Fotografiar planetas requiere valorar los límites que la rotación planetaria impone al tiempo total de integración que resulta de sumar la exposición de numerosas fotografías, sobre todo para el caso de Júpiter y en menor medida para Saturno y Marte.
La técnica habitual para obtener detalles de los discos planetarios consiste en apilar fotografías de corta exposición (subexposiciones) obtenidas grabando un vídeo webcam o por otros medios (puedes ver un ejemplo en Cómo fotografiar Júpiter). Como los planetas rotan mientras se realiza la grabación, la pregunta inmediata es durante cuánto tiempo pueden captarse fotogramas antes de que ese movimiento afecte a la nitidez de la fotografía.
Puedes aproximar el tiempo de exposición (en minutos) para tu equipo de la siguiente manera:
- Multiplica 3939 por tu tamaño de pixel (en micras) y por el período de rotación del planeta (en horas)
- Mutiplica tu longitud focal efectiva (en milímetros) por el diámetro aparente del planeta (en segundos de arco)
- Divide el primer valor por el segundo
También puedes utilizar esta calculadora del límite de exposición por rotación planetaria. Los siguientes apartados están dedicados a explicar esta fórmula.
Velocidad media de rotación planetaria
Las imágenes de la Tierra suelen representarse como un disco con el polo Norte situado en el extremo superior y el polo Sur en su extremo inferior.
Si representamos cualquier planeta de la misma manera, los detalles de su superficie se desplazarán de un borde a otro conforme el planeta rota. Naturalmente la velocidad será mayor en el ecuador del planeta, ya que debe recorrerse todo el diámetro del disco, mientras que cerca de los polos habrá menor desplazamiento.
Puedes calcular la velocidad media de desplazamiento en el ecuador conociendo el tamaño del diámetro del planeta y su período de rotación. El diámetro cambia conforme los planetas varían su distancia a la Tierra, pero ambos datos pueden conocerse fácilmente consultando efemérides astronómicas o bien utilizando el software gratuito Stellarium (basta buscar el planeta pulsando ctrl-F para obtener su «Diámetro aparente» y «Día solar medio»).
Por ejemplo Júpiter tiene en estos momentos un diámetro aparente de 44 segundos de arco y Saturno de 16 segundos (38 incluyendo sus anillos). Ambos tiene un periodo de rotación de unas 10 horas. Como tu imagen solo capta la mitad visible del disco planetario, en ambos casos un punto recorre el ecuador planetario en unas 5 horas (300 minutos). La velocidad media resultante es 44 / 300 = 0.1467 segundos de arco cada minuto en el caso de Júpiter y 16 / 300 = 0.0533 segundos de arco por minuto para Saturno. La fórmula de esta velocidad es sencillamente v = 2 D / T, donde D es el diámetro aparente del planeta (en segundos de arco) y T el periodo de rotación del mismo (en horas).
Para calcular los límites de exposición fotográfica puedes medir cuánto tardará un punto de tu imagen en desplazarse de un pixel del sensor fotográfico al pixel contiguo. La escala de pixel de tu imagen, es decir, los segundos de arco que abarca cada pixel de la imagen, puede calcularse multiplicando el tamaño de píxel de tu sensor (en micras) por 206,26 y dividiendo el resultado por la longitud focal efectiva de tu equipo (en milímetros).
Por ejemplo en mi caso utilizo habitualmente un telescopio de 750mm de longitud focal con una lente de Barlow 3x, lo que me da una longitud focal efectiva de 750 x 3 = 2.250mm. Si acoplo una cámara con píxeles de 5,6 micras, mi escala de píxel es 5,6 x 206,26 / 2,250 = 0,51 segundos de arco por píxel.
Para finalizar basta con dividir la velocidad media de rotación por la escala de píxel. Siguiendo con el ejemplo, un punto en el ecuador de Júpiter tardará 0.51 / 0.1467 = 3.5 minutos en desplazarse un pixel. Y para el caso de Saturno tendremos 0.51 / 0.0533 = 9.6 minutos de exposición máxima.
Aunque esto es una primera aproximación, los tiempos de integración calculados de esta manera puede resultar en pérdidas de nitidez. El motivo es que los puntos del disco planetario no se desplazan sobre la imagen a velocidad constante como veremos en el próximo apartado.
Velocidad instantánea de rotación planetaria
Los radares de carretera miden tu velocidad en un instante concreto sin importarles la velocidad media que hayas mantenido durante tu trayecto y lo mismo le sucede a la nitidez de una fotografía sigue: se deteriorará si la velocidad instantánea de un punto es excesiva, sin importar su velocidad media.
Si observas una fotografía de la Luna, sus detalles parecen deformarse y apelotonarse en la periferia del disco debido a las deformaciones que impone la fotografía al proyectar una semiesfera sobre un plano. De la misma forma la resolución espacial en cualquier planeta es menor conforme te acercas al limbo, por lo que es preferible que los detalles que pretendes fotografiar se encuentren centrados. Sin embargo, por el mismo motivo, en el centro del disco los detalles se desplazan más rápido por el plano fotográfico que en los bordes, lo que afecta al tiempo de exposición máximo que puedes permitirte en tu fotografía.
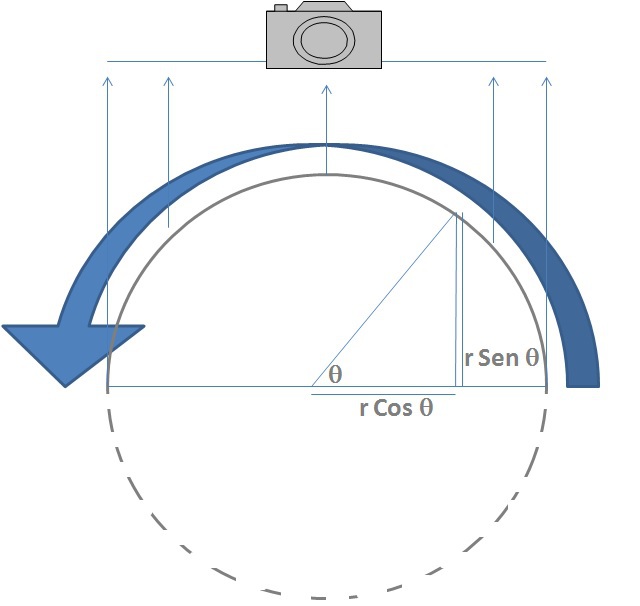
Los cálculos de velocidad instantánea son algo más sofisticados que los de velocidad media pero tan solo requieren calcular la derivada del espacio como función del tiempo. Si te enfocas en el ecuador del planeta, puedes imaginarlo como una semicircunferencia que, al fotografiarla, se proyecta sobre un segmento equivalente al diámetro de la misma, conforme ilustra la imagen que encabeza esta entrada.
Para realizar cálculos puedes expresar los puntos de esa circunferencia en coordenadas polares (r cos Theta, r sen Theta), donde r es el radio de la circunferencia y Theta el ángulo que forma el eje horizontal con la línea que une el origen de coordenadas con ese punto. Theta varía de forma constante con el tiempo y completa una revolución en cada periodo T de rotación planetaria, así que puedes expresarlo en función del tiempo y en radianes como Theta (t) = (2Pi/T) t. El radio r vendría expresado en segundos de arco como la mitad del diámetro aparente del planeta. Ahora bien, lo que te interesa a efectos de fotografía no es tanto la posición del punto sobre la circunferencia como la proyección de su posición sobre el plano fotográfico, así que puedes proyectar la circunferencia sobre el eje horizontal quedándote con la primera componente de las coordenadas polares. Sustituyendo Theta puedes escribir la posición proyectada del punto como s(t) = r cos ((2Pi/T) t), lo que te permite calcular la velocidad v en cada punto como derivada de la expresión anterior, es decir, v(t) = (2Pi/T) r sen ((2Pi/T) t).
El galimatías anterior se traduce en que la velocidad es nula cuando t=0 o cuando t=T/2, es decir, en el instante en que un punto se encuentra en el limbo del planeta no se mueve en la fotografía, ya que su velocidad está dirigida «hacia el fondo» de la imagen (o «desde el fondo»). Y la velocidad máxima se produce cuando la función seno toma valor 1, es decir cuando t =T/4 y el punto se encuentra cruzando el meridiano central del planeta. En ese momento la velocidad es v = (2Pi/T) r = Pi D/T.
Comparando con la fórmula de velocidad media, tenemos que la velocidad instantánea supera a la velocidad media en un factor Pi/2, es decir, es un 57% mayor.
Para ver un ejemplo, en el caso de Júpiter tendríamos una velocidad de 44xPi/600 = 0,23 segundos de arco por minuto y en el caso de Saturno 16xPi/600 = 0,08. A partir de aquí puedes aproximar el tiempo de exposición aplicando la escala de píxel de la misma manera que en el apartado anterior, que arrojaría un resultado de 0,51/0,23=2,21 minutos para Júpiter y 0,51/0,16=6,08 para Saturno.
Si quieres ser absolutamente pulcro con el cálculo del tiempo de exposición puedes calcular cuánto tarda en desplazarse un punto por un pixel cuando la velocidad es máxima, es decir, cuando está centrado sobre el meridiano central del planeta. Para esto puedes utilizar la función de posición espacial s(t) = r cos ((2Pi/T) t) y calcular el momento en que ese punto entra en el píxel y sale de él. Con una escala de pixel de 0.51 segundos de arco, el punto ingresaría cuando s=0.51/2 y saldría cuando s= – 0.51/2 y despejando la función s(t) los valores de t serían t=148,8931 minutos al entrar y t=151,1069 al salir. El tiempo transcurrido es por tanto 12.21 minutos aproximadamente, un valor igual que el obtenido en el párrafo anterior, aunque si calculas suficientes decimales obtendrás una diferencia debida a que la velocidad instantánea no se mantiene en su valor máximo más que un instante y comienza a disminuir conforme el punto atraviesa el pixel. En cualquier caso, esto no tiene mayores implicaciones prácticas.
Como conclusión, el tiempo de exposición estimado con la velocidad instantánea de rotación es menor al estimado con la velocidad media. A pesar de la reducción sufrida, la buena noticia es que el resultado aún te ofrece margen para realizar vídeos planetarios con fotogramas suficientes para el apilado y sin correr el riesgo de que la rotación planetaria haga perder nitidez a tu imagen. Ten en cuenta sin embargo que cuanto mayor sea la resolución que utilices, menor será el tiempo de exposición del que dispondrás, por lo que en alta resolución puede ser buena idea sobrepasar estos límites a cambio de obtener suficientes datos para integrar.
Inclinación orbital e inclinación axial
Si aún te interesa profundizar un poco más en las implicaciones de la rotación planetaria, este apartado cubre un aspecto obviado en los apartados anteriores: los planetas no siempre se muestran con sus polos situados en el limbo del disco.
Ya sabes que los planetas orbitan alrededor del sol por un plano similar al de la Tierra, pero no exactamente el de la eclíptica. Además, el eje de rotación de algunos planetas está inclinado respecta a su plano orbital. En la Tierra esta inclinación es la causante de las estaciones, al igual que en otros planetas. Respecto a las implicaciones en fotografía, esto hace que los planetas vayan cabeceando lentamente conforme orbitan alrededor delo sol, lo que te permite fotografiar sus polos si eliges el momento adecuado. Puedes ver un ejemplo de este movimiento del eje en esta maravillosa composición de imágenes de Saturno realizada por Damian Peach con tomas obtenidas durante 11 años.
Las siguiente implicación para tu fotografía es que los puntos de la imagen se desplazan de un modo diferente al considerado hasta hora, ya que por ejemplo el ecuador del planeta deja de ser un segmento que atraviesa el disco planetario de un lado a otro. La proyección de una circunferencia como el ecuador planetario sobre un plano inclinado da como resultado una elipse, lo que complica un poco el cálculo de curvas de posición y velocidad.
Si necesitas realizar cálculos detallados por algún motivo puedes partir de una esfera tridimensional centrada en el origen de coordenadas y que rota sobre un eje determinado por un vector unitario U = (Ux, Uy, Uz). Si aplicas una matriz de rotación tridimensional a la esfera obtendrás la trayectoria tridimensional de un punto alrededor de esa esfera, que posteriormente puedes proyectar sobre el plano horizontal, obteniendo una elipse. La derivada de las componentes de la elipse te daría el vector de velocidad en el plano fotográfico y su módulo te ofrecería el valor de velocidad necesario para calcular el tiempo de exposición.
Por fortuna, el tiempo límite de exposición no varía respecto al calculado en el apartado anterior, por lo que no es necesario entrar en complejidades salvo que necesites obtener detalles de algún punto concreto del planeta por algún motivo. Al igual que sucedía en el apartado anterior, la velocidad es máxima en la imagen cuando el vector tridimensional de velocidad es paralelo al plano fotográfico, es decir, horizontal. En ese instante, el módulo de su proyección sobre el plano es igual a su módulo en tres dimensiones, ya que la componente vertical es nula. Y en tres dimensiones el módulo del vector es máximo en el ecuador planetario y toma el mismo valor que ya obtuviste en el apartado anterior v = Pi D / T.
Para ilustrar esta conclusión en un caso concreto, podríamos volar hasta situarnos sobre el polo de un planeta y fotografiarlo desde arriba, con lo cual el ecuador planetario se convertiría en la circunferencia que delimita el disco planetario. La longitud de esa circunferencia es el resultado de multiplicar su diámetro por el número Pi. Y la velocidad de desplazamiento sería por tanto el resultado de dividir ese valor por el período de rotación del planeta. En este caso específico la velocidad instantánea es constante y coincide con la velocidad media: v= Pi D / T.
Mitigación de los efectos de rotación mediante procesado
La limitación del tiempo de exposición juega en contra de la calidad del resultado fotográfico, ya que para lograr fotografías de calidad es preferible apilar tantos fotogramas como sea posible, lo que requiere integrar tiempos largos. Si utilizas una cámara monocroma con filtros para la captación de color el problema se agrava aún más ya que cada canal se grabará en periodos diferentes, lo que puede producir cromatismo en la imagen. Sobre todo en el caso de Júpiter las cosas se ponen complicadas, ya que su mayor tamaño y rápida rotación permiten resoluciones altas pero agravan los problemas de exposición. Además Júpiter ofrece un elevado nivel de pequeños detalles que pueden deteriorarse rápidamente por efecto de la rotación.
Por suerte puedes utilizar herramientas de procesado para mitigar los efectos de la rotación, como por ejemplo el software gratuito WinJupos. En líneas generales este software u otros similares toman cada fotograma y simulan la rotación del planeta de forma algorítmica para lograr que todos ellos estén alineados, es decir, des-rotan las imágenes. Una vez realizada esta operación los fotogramas pueden apilarse sin sufrir los temidos efectos que nos ocupan.
Sin embargo, como sucede siempre con las operaciones de procesado, el demonio está en los detalles. Además de las complejidades discutidas arriba, implícitas en cualquier cálculo de rotación, siempre se sufre deterioro en la información al realizar operaciones de procesado. Recuerda por ejemplo que un pixel en el limbo del planeta tiene una resolución espacial menor que un pixel en el centro de la imagen. En teoría sería posible des-rotar ese píxel y llevarlo al centro del planeta, pero la pérdida de resolución no tiene solución, ya que la información sencillamente no está disponible en la imagen original. Esto impone limitaciones al tiempo de exposición durante el que el procesamiento ofrece ventajas.
Además de esto, la iluminación en la esfera del planeta no es homogénea, sino que disminuye al alejarse del centro. Este efecto también es tenido en cuenta por WinJupos, pero de nuevo el cálculo se realiza mediante la aproximación del comportamiento de una esfera idealizada.
Y por supuesto, el software debe hacer frente a la calidad inicial de tus imágenes, que siempre estarán perturbadas por todo tipo de ruido, efectos de seeing o visibilidad atmosférica, etc, lo que dificulta aún más la ejecución de un procesado preciso.
Aún con todas estas dificultades, WinJupos y otros sofware realizan una tarea encomiable y permiten mejorar notablemente la calidad del resultado final frente a imágenes no des-rotadas. Conviene sin embargo ser conscientes de las dificultades involucradas y de las limitaciones de las herramientas disponibles para no forzarlas más allá de sus límites, lo que tendría un efecto negativo en la calidad de tus fotografías.